首先需要了解几个概念:
对于一个标准的线性规划问题
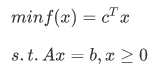
设A为m×n满秩的矩阵,将它分块为A=[B N],其中B为m×m非奇异矩阵,x按B和N的列选择划分成x=(xB xN)T
于是Ax=b可以写成

因此有

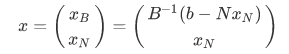
取xN=0,有
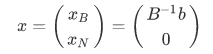
这样的解叫做基本解,xN、xB分别叫非基本变量和基本变量,N、B分别是基矩阵、非基矩阵
满足非负可行条件的基本解叫做基本可行解
可以证明,每一个基本可行解对应可行域中的一个顶点
单纯形法是一种广泛应用的线性规划方法,其思想是在顶点上逐个检验最优性,然后寻找相邻的更优顶点,直到确定问题的最优解
在这个算法中,关键的两步是1)检验解是否是最优解,2)寻找下一个基本可行解
这里有几个新的概念:
- 在检验最优解这一步有单纯形乘子、价值系数向量 ,其含义见算法
- 在寻找下一个基本可行解这一步,做法是把原非基矩阵的一列(入基变量)和原矩阵的一列(出基变量)交换
单纯形法的步骤如下:

下面给出单纯形法的python实现:
1 # coding=utf-8 2 from numpy import * 3 4 5 def simple(c, A, b): 6 m = min(A.shape) 7 n = max(A.shape) 8 M = range(0, n) 9 E = range(0, m)10 B = A[:, E]11 I = setdiff1d(M, E)12 N = A[:, I]13 i = 114 x = arange(0, n).astype(float)15 while True:16 if linalg.matrix_rank(B) == m:17 x[E] = dot(linalg.inv(B), b).flatten()18 x[I] = arange(0, n - m)19 if min(x) >= 0:20 break21 E[m - i] += 122 I = setdiff1d(M, E)23 N = A[:, I]24 B = A[:, E]25 i = i + 126 # -------27 # E=[2,3,4]28 # I=[0,1]29 # N = A[:, I]30 # B = A[:, E]31 # x=array([0.,0.,3.,2.,16.])32 # -------33 cb = c[E]34 cn = c[I]35 # 单纯形乘子36 y = dot(linalg.inv(B.T), cb)37 # 简约价值系数38 cv = cn - dot(N.T, y)39 eps = 10 ** (-7)40 r = b41 while min(cv) < 0:42 p = I[where(cv == min(cv))[0][0]]43 ap = dot(linalg.inv(B), A[:, p])44 bq = r[ap > eps] / ap[ap > eps]45 bq = min(bq)46 q = E[where(r / ap == bq)[0][0]]47 out = where(array(E) == q)[0][0]48 enter = where(array(I) == p)[0][0]49 E[out] = p50 I[enter] = q51 N = A[:, I]52 B = A[:, E]53 x[E] = dot(linalg.inv(B), b).flatten()54 r = x[E]55 x[I] = zeros(n - m)56 cb = c[E]57 cn = c[I]58 y = dot(linalg.inv(B.T), cb)59 cv = cn - dot(N.T, y)60 print(x)61 62 63 c = array([-2, -3, 0, 0, 0])64 A = array([[-1, 1, 1, 0, 0], [-2, 1, 0, 1, 0], [4, 1, 0, 0, 1]])65 b = array([3, 2, 16])66 simple(c, A, b)
运行结果:

即x1=2.6 x2=5.6 x3=0 x4=1.6 x5=1 是该问题的最优解